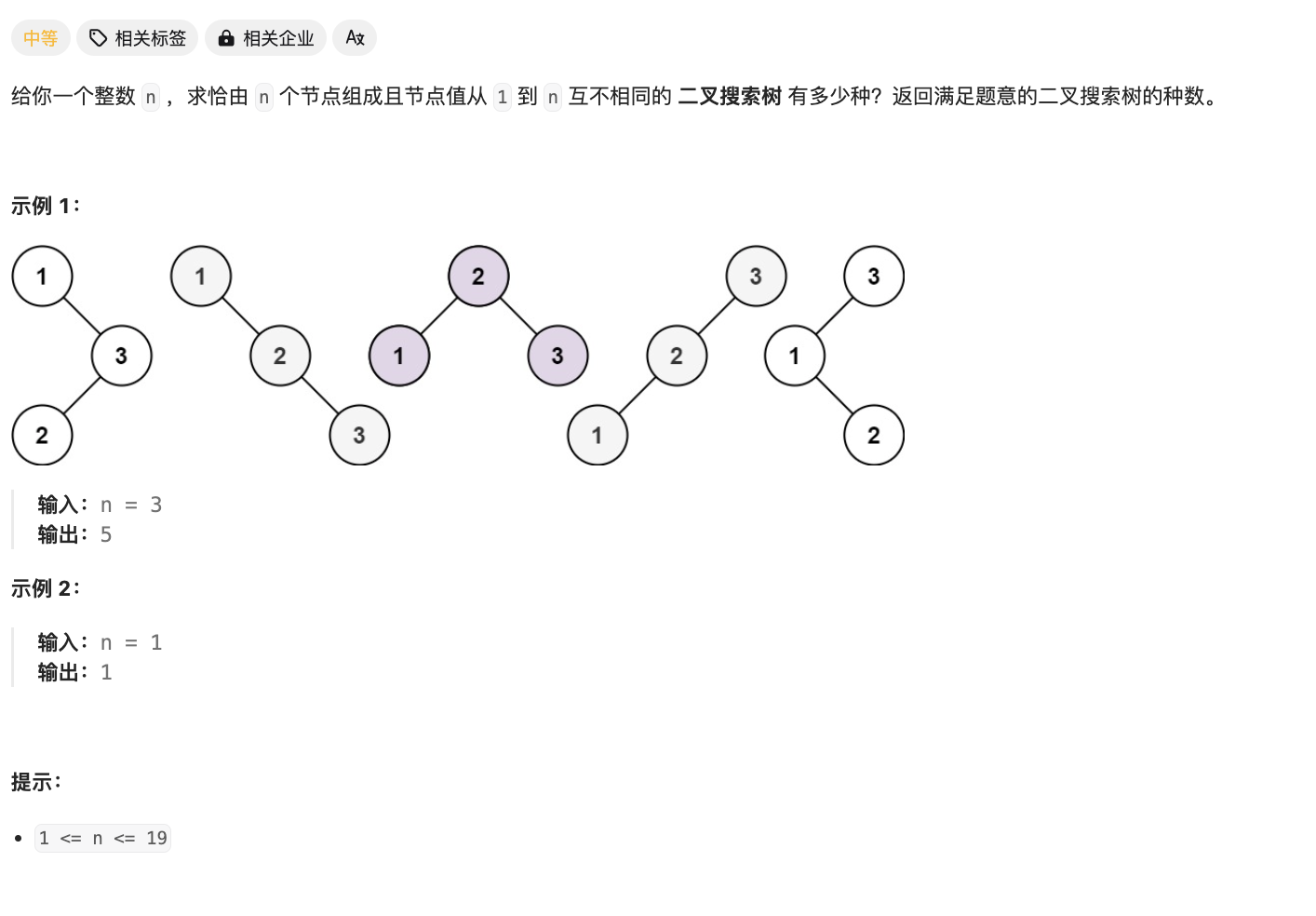
题目
解题
排列组合 感觉还是回溯解
不同的二叉搜索树是一道动态规划的经典问题。这个问题要求计算由 1 到 n 组成的不同的二叉搜索树的数量。我们可以使用动态规划来解决这个问题。下面是用 Python 实现的解题代码:
def numTrees(n):
if n == 0 or n == 1:
return 1
dp = [0] * (n + 1)
dp[0] = 1
dp[1] = 1
for i in range(2, n + 1):
for j in range(1, i + 1):
dp[i] += dp[j - 1] * dp[i - j]
return dp[n]
在这段代码中,我们使用了一个数组 dp 来保存不同数量节点所构成的二叉搜索树的数量。我们首先初始化 dp[0] 和 dp[1] 为 1,因为构成空树或者只有一个节点的树的数量都是 1。然后我们使用两层循环,外层循环遍历节点的数量,内层循环遍历每个节点作为根节点时的情况。我们累加每种情况下左子树和右子树构成的二叉搜索树的数量,最终得到以当前节点数量构成的所有二叉搜索树的数量。
首先,我们初始化 dp 数组为 [0, 0, 0, 0],表示节点数量为 0 到 3 的二叉搜索树数量。然后我们开始按照步骤进行动态规划。
1. 初始化:dp[0] = 1, dp[1] = 1。
2. 对于节点数量为 2 的情况,我们计算以 1 和 2 为根节点的二叉搜索树数量:
- 以 1 为根节点:左子树为空,右子树有 1 个节点,所以数量为 dp[0] * dp[1] = 1 * 1 = 1。
- 以 2 为根节点:左子树有 1 个节点,右子树为空,所以数量为 dp[1] * dp[0] = 1 * 1 = 1。
因此,dp[2] = 1 + 1 = 2。
3. 对于节点数量为 3 的情况,我们计算以 1、2 和 3 为根节点的二叉搜索树数量:
- 以 1 为根节点:左子树为空,右子树有 2 个节点,所以数量为 dp[0] * dp[2] = 1 * 2 = 2。
- 以 2 为根节点:左子树有 1 个节点,右子树有 1 个节点,所以数量为 dp[1] * dp[1] = 1 * 1 = 1。
- 以 3 为根节点:左子树有 2 个节点,右子树为空,所以数量为 dp[2] * dp[0] = 2 * 1 = 2。
因此,dp[3] = 2 + 1 + 2 = 5。
最终,我们得到节点数量为 3 时的 dp 数组为 [1, 1, 2, 5],表示节点数量为 0 到 3 的二叉搜索树数量分别为 1, 1, 2, 5。希望这个图示能够帮助你更好地理解动态规划的执行步骤!