枚举算法

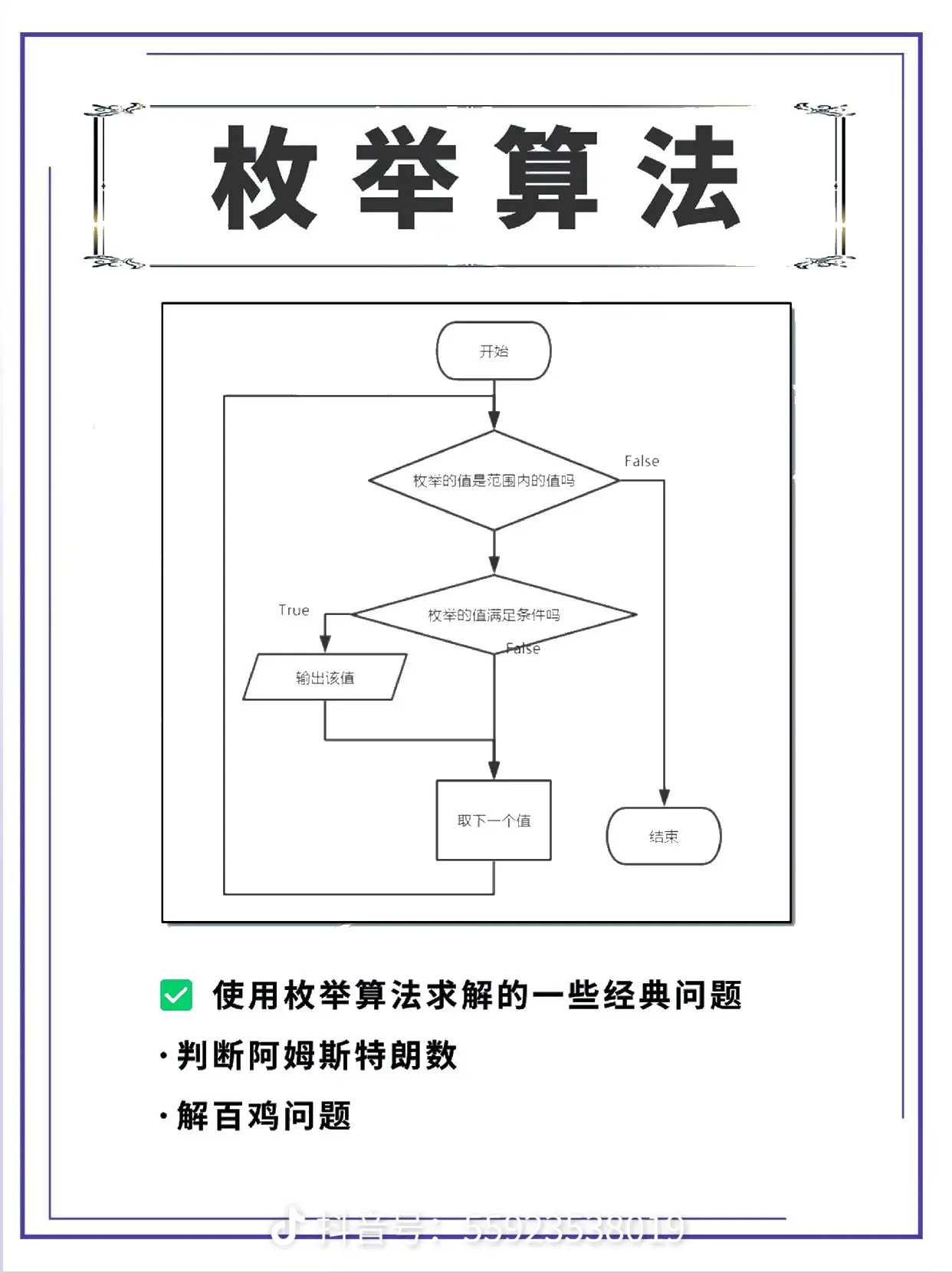
Pasted image 20240118210232.png

解题模板

枚举算法，也称为暴力搜索算法，是一种直接的解决问题的方法，它通过穷举所有可能的候选解并检查每个候选解是否满足问题的约束条件来找到问题的解。枚举算法通常用于解决组合问题，如排列、组合、子集生成等，以及其他需要尝试所有可能性的问题。

枚举算法的一般步骤包括：

定义解空间：明确问题的解空间，即所有可能的候选解的集合。
确定枚举顺序：根据问题的具体情况，确定一个合理的枚举顺序，以便系统地遍历所有候选解。
检查候选解：对于每个候选解，检查它是否满足问题的约束条件。
记录有效解：如果候选解满足所有约束条件，则将其记录为有效解，或者根据问题的要求对其进行处理。
返回结果：根据问题的要求，返回最终的结果，可能是所有有效解的集合、最优解或者满足条件的解的数量等。

枚举算法的简单模板如下：

def enumeration_algorithm(problem):
    # 初始化结果集
    results = []

    # 遍历解空间中的所有候选解
    for candidate in solution_space(problem):
        # 检查候选解是否满足问题的约束条件
        if is_valid_solution(candidate, problem):
            # 如果满足条件，则记录候选解
            results.append(candidate)
            # 根据问题要求，可能需要对候选解进行额外的处理
            # ...

    # 返回最终结果
    return results

# 辅助函数：生成解空间中的候选解
def solution_space(problem):
    # 实现生成解空间的逻辑
    pass

# 辅助函数：检查候选解是否有效
def is_valid_solution(candidate, problem):
    # 实现检查逻辑
    pass

枚举算法非常直观，但其效率通常较低，特别是当解空间非常大时，可能需要非常长的时间来找到解。因此，在实践中，我们通常会尝试优化枚举过程，例如使用剪枝技术来减少不必要的枚举，或者使用更高效的算法（如动态规划、贪心算法等）来解决特定问题。

# 应用场景

枚举算法是一种直接的计算方法，它通过尝试所有可能的候选解并检查每个候选解是否满足问题的要求来找到问题的解。在LeetCode上，枚举算法通常用于以下类型的问题：

全排列问题：
- 需要找出一个集合的所有排列方式（如LeetCode 46题：全排列）。
组合问题：
- 需要找到所有特定大小的组合（如LeetCode 77题：组合）。
子集问题：
- 需要列出一个集合的所有可能子集（如LeetCode 78题：子集）。
暴力搜索问题：
- 对于某些问题，可能没有明显的算法策略，需要通过尝试所有可能的情况来找到解答（如LeetCode 37题：解数独）。
位运算问题：
- 利用位操作枚举子集或特定条件下的数（如LeetCode 78题：子集，通过位运算枚举）。
回溯问题：
- 回溯算法是一种通过枚举所有可能的候选解来寻找所有解的方法，通常用于解决组合问题、分割问题、子集问题和排列问题等（如LeetCode 22题：括号生成）。
数独和填字游戏：
- 通常需要枚举所有可能的填充方式来解决问题（如LeetCode 37题：解数独）。
模拟问题：
- 一些问题可能需要模拟所有可能的情况或步骤来找到答案（如LeetCode 289题：生命游戏）。

枚举算法的优点是它简单直观，易于实现，对于问题规模较小的情况通常很有效。然而，枚举算法的缺点是它的时间复杂度通常较高，对于规模较大的问题可能不实用，因为可能需要花费过长的时间来处理所有可能的情况。因此，在使用枚举算法时，通常需要考虑是否可以通过剪枝（在搜索过程中排除一些不可能的情况）或其他优化方法来减少计算量。